はじめに
- THREE.Mesh はポリゴン(面)を使ってジオメトリを描画
*通常の3Dモデルやオブジェクトを表示する際に使用 - THREE.Pointsはジオメトリの頂点を点として描画
*線や面を作らず、点だけを表示する場合
- ワールド座標とローカル座標
THREE.Mesh と THREE.Points の両方にワールド座標とローカル座標の概念がある- ローカル座標:オブジェクト自体の配置例えば、THREE.Mesh や THREE.Points で指定する位置(position)、回転(rotation)、スケール(scale)はローカル座標系で定義
- ワールド座標:オブジェクトがシーン全体(ワールド)に対してどの位置にあるか
- 法線(normal )ベクトル
THREE.Mesh の表面の各頂点や面がどの方向を向いているかを示すもので
特にライティングや反射などの効果を計算する際に使われる
備考:Three.jsシェーダーで使用される主要な変数( uniform変数、attribute 変数、組み込み変数)
主なuniform変数(シェーダーがレンダリングされる際に Three.js が自動でシェーダーに渡す)
- modelMatrix(モデル行列)
頂点シェーダーのみで使用
モデルのローカル座標からワールド座標を計算するための変換行列 - viewMatrix(ビュー行列)
頂点シェーダーのみで使用
ワールド座標からカメラ空間の座標を計算するための変換行列 - projectionMatrix(投影行列)
頂点シェーダーのみで使用
カメラ空間での3D座標を2Dスクリーン座標に投影するための変換行列 - cameraPosition
頂点シェーダーとフラグメントシェーダーで使用
ワールド空間におけるカメラの絶対位置
主なattribute変数(頂点ごとのデータ)
頂点シェーダーのみで使用
- position: 各頂点の3D位置(vec3)
- uv:各頂点におけるテクスチャ座標(vec2)
- normal:各頂点の法線ベクトル(vec3)
- color:各頂点の色(vec3)
gl_で始まる組み込み変数の例
- 頂点シェーダーで使われる組み込み変数
- gl_Position:頂点の最終的な位置(必ず出力する)
- gl_PointSize:点(ポイント)の大きさ
- フラグメントシェーダーで使われる組み込み変数
- gl_FragColor:最終的に描画されるフラグメントの色
- gl_FragCoord:フラグメントのウィンドウ座標(X、Y、Z)
- gl_FrontFacing:フラグメントが表側にあるかを示すブール値
- gl_FragDepth:フラグメントの深度値をオーバーライドするのに使用
*デフォルトではgl_FragCoord.zが使われる
THREE.Mesh
JSのセットアップ
import * as THREE from 'three'
import { OrbitControls } from 'three/examples/jsm/controls/OrbitControls.js'
import { GLTFLoader } from 'three/addons/loaders/GLTFLoader.js' //モデルをロードする場合
import vertexShader from './vertex.glsl'
import fragmentShader from './fragment.glsl'
const canvas = document.querySelector('.webgl')
const scene = new THREE.Scene()
const sizes = {
width: window.innerWidth,
height: window.innerHeight,
pixelRatio: Math.min(window.devicePixelRatio, 2)
}
const camera = new THREE.PerspectiveCamera(25, sizes.width / sizes.height, 0.1, 100)
camera.position.set(0, 0, 8)
scene.add(camera)
// Controls
const controls = new OrbitControls(camera, canvas)
controls.enableDamping = true
const renderer = new THREE.WebGLRenderer({
canvas: canvas,
antialias: true
})
renderer.setSize(sizes.width, sizes.height)
renderer.setPixelRatio(sizes.pixelRatio)
const material = new THREE.ShaderMaterial({
vertexShader: vertexShader,
fragmentShader: fragmentShader,
uniforms:{
//uTimeはグリッチエフェクトで利用
uTime: { value: 0 },
//uResolutionはハーフトーンシェーディングで利用
uResolution: {value: new THREE.Vector2(sizes.width*sizes.pixelRatio, sizes.height*sizes.pixelRatio) },
},
// transparent:true, //フレネル効果では有効に
// depthWrite: false, //フレネル効果では有効に
// side: THREE.DoubleSide, //フレネル効果では有効に
})
//ジオメトリ
const torusKnot = new THREE.Mesh(
new THREE.TorusKnotGeometry(0.6, 0.25, 128, 32),
material
)
scene.add(torusKnot)
//モデル
// const gltfLoader = new GLTFLoader()
// let model = null
// gltfLoader.load(
// '/model.glb',(gltf) =>{
// model = gltf.scene
// model.traverse((child) =>{
// if(child.isMesh)
// child.material = material
// })
// model.position.set(-1, 0, 0)
// scene.add(model)
// }
// )
function handleResize(){
sizes.width = window.innerWidth
sizes.height = window.innerHeight
sizes.pixelRatio = Math.min(window.devicePixelRatio, 2)
//uResolutionはハーフトーンシェーディングで利用
material.uniforms.uResolution.value.set(sizes.width*sizes.pixelRatio, sizes.height*sizes.pixelRatio)
camera.aspect = sizes.width / sizes.height
camera.updateProjectionMatrix()
renderer.setSize(sizes.width, sizes.height)
renderer.setPixelRatio(sizes.pixelRatio)
}
const clock = new THREE.Clock()
const tick = () =>{
controls.update()
const elapsedTime = clock.getElapsedTime()
//uTimeはグリッチエフェクトで利用
material.uniforms.uTime.value = elapsedTime
torusKnot.rotation.x = - elapsedTime * 0.5
torusKnot.rotation.y = elapsedTime * 1
// if(model){
// model.rotation.x = - elapsedTime * 0.1
// model.rotation.y = elapsedTime * 0.2
// }
renderer.render(scene, camera)
window.requestAnimationFrame(tick)
}
handleResize()
tick()
window.addEventListener('resize', handleResize)
ワールド座標とローカル座標
//頂点シェーダーから送られたvPositionをフラグメントの色に割り当てる
varying vec3 vPosition;
void main(){
gl_FragColor = vec4(vPosition, 1.0);
}ワールド座標
modelPosition(ワールド座標での頂点の位置)のxyzをフラグメントシェーダーに送る
*オブジェクトが動いたり回転してもパターンが「固定」される
varying vec3 vPosition;
void main(){
// モデル行列を使って、ローカル座標(position)をワールド座標に変換
vec4 modelPosition = modelMatrix * vec4(position, 1.0);
gl_Position = projectionMatrix * viewMatrix * modelPosition;
//modelPosition.xyzをvPositionに割り当てる
vPosition = modelPosition.xyz;
}
ローカル座標
positionを(ローカル座標での頂点の位置)をフラグメントシェーダーに送る
*オブジェクトに「追従する」ため、オブジェクトとパターンが一緒に動く
varying vec3 vPosition;
void main(){
vec4 modelPosition = modelMatrix * vec4(position, 1.0);
gl_Position = projectionMatrix * viewMatrix * modelPosition;
//positionをvPositionに割り当てる
vPosition = position;
}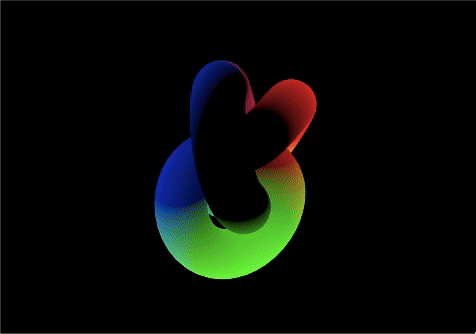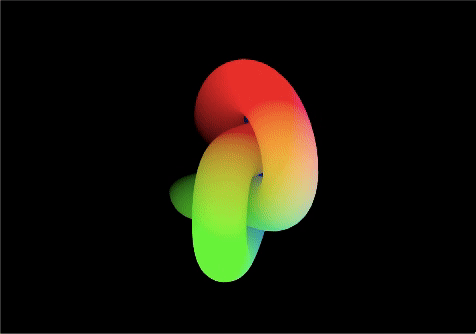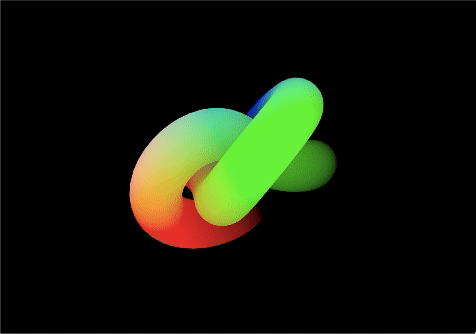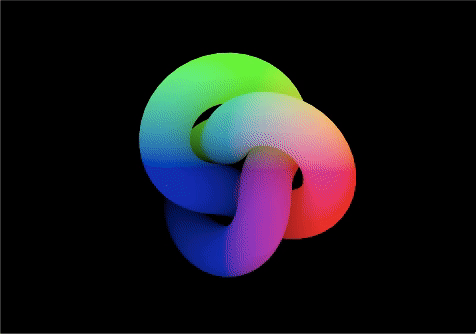
グリッチエフェクト
デジタルデータが壊れたような見た目やノイズ、乱れを再現するアニメーション
*modelPositionの時間経過でアニメーションする
varying vec3 vPosition; //フラグメントシェーダーで利用する
uniform float uTime;
// 2次元のランダムノイズ関数
float random2D(vec2 value){
return fract(sin(dot(value, vec2(12.9898,78.233))) * 43758.5453123);
}
void main(){
vec4 modelPosition = modelMatrix * vec4(position, 1.0);
// y座標に基づくタイミングの遅延で、下から上にグリッチがかかる
float glitchTime = uTime - modelPosition.y;
// sin関数を使ってグリッチの強さを計算し、複雑さを加える
float glitchStrength = sin(glitchTime) + sin(glitchTime * 3.45) + sin(glitchTime * 8.76);
glitchStrength /= 3.0; // 3で割って平均化
// エフェクトの強度を調整
glitchStrength *= 0.2;
// x座標にランダムなノイズを加える(ランダムに揺らす)
modelPosition.x += (random2D(modelPosition.xz + uTime) - 0.5) * glitchStrength;
// z座標にも同様にランダムなノイズを加える
modelPosition.z += (random2D(modelPosition.zx + uTime) - 0.5) * glitchStrength;
gl_Position = projectionMatrix * viewMatrix * modelPosition;
/*
1. Y軸方向にもグリッチエフェクトを適用
modelPosition.y += (random2D(modelPosition.xy + uTime) - 0.5) * glitchStrength;
2. グリッチエフェクトのタイミングを変更
float glitchTime = uTime; // y座標に依存せず、時間経過で全体に均等にグリッチが適用されます。
3. エフェクトの出現頻度を調整
glitchStrength = smoothstep(0.3, 1.0, glitchStrength);
4. グリッチの強度をランダムに変化させる
グリッチの強さを固定せず、強度を時間や位置に依存して変化させる
glitchStrength *= random2D(modelPosition.xy + uTime * 0.1); // ノイズで強度を変化させる
*/
vPosition = modelPosition.xyz;
}
フレネル効果
フレネル効果は、視点の角度に基づく見え方
視線に対して物体がどの角度にあるかで見え方が変わる
斜めから見ると反射が強くなる(見える)、正面から見ると反射が弱くなる(見えない)
*物体のエッジや斜めの角度で反射が強くなる
*用途:ガラス、水、半透明の素材の反射など
法線ベクトルと視点ベクトルのドット積を計算する
- 法線ベクトルと視点ベクトルが同じ方向を向いている場合は:1
- 垂直の場合:0
- 反対の場合:-1
- 中間の値は補間される
// ワールド座標での法線ベクトルの計算(平行移動は無視するので0.0)
vec4 modelNormal = modelMatrix * vec4(normal, 0.0);
// フラグメントシェーダーにワールド座標系の法線ベクトルと位置をを送る
vNormal = modelNormal.xyz;フラグメントシーダーではワールド座標での「法線ベクトルと頂点の位置」が必要
varying vec3 vPosition; // フラグメントシェーダーに送るワールド座標での頂点の位置
varying vec3 vNormal; // フラグメントシェーダーに送るワールド座標での法線ベクトル
void main(){
// モデル行列を使って、ローカル座標(position)をワールド座標に変換
vec4 modelPosition = modelMatrix * vec4(position, 1.0);
// ワールド座標での法線ベクトル: 正しい方向の法線を計算(平行移動は無視するので0.0)
vec4 modelNormal = modelMatrix * vec4(normal, 0.0);
// 頂点をスクリーンに投影
gl_Position = projectionMatrix * viewMatrix * modelPosition;
// フラグメントシェーダーにワールド座標系の法線ベクトルと位置をを送る
vNormal = modelNormal.xyz;
vPosition = modelPosition.xyz;
}varying vec3 vPosition;
varying vec3 vNormal;
void main(){
// 視点ベクトルの正規化(カメラ位置から頂点までのベクトル)
vec3 viewDirection = normalize(vPosition - cameraPosition);
// 法線ベクトルを正規化
vec3 normal = normalize(vNormal);
/*
THREE.DoubleSideオプションを考慮する場合、裏側もレンダリングされるようになり
法線ベクトルの向きが裏側では反転するため、フレネル効果の計算が正しく機能しない可能性がある
gl_FrontFacingで裏面かどうか判定して 裏面の法線は反転させる
*/
if (!gl_FrontFacing) {
normal = -normal; // 裏面の場合、法線を反転させる
}
// 法線ベクトルと視線方向ベクトルのドット積を計算
float fresnel = dot(normal, viewDirection);
/*
フレネル効果を調整(0から1の範囲にスケール)
ドット積の計算結果は-1から1の範囲を取りますが、透明度に使用する際は0から1の範囲にする
*/
fresnel = clamp((fresnel + 1.0) / 2.0, 0.0, 1.0);
// フレネル効果を強調(オプション)
//fresnel = pow(fresnel, 2.0);
// フレネル効果に基づいた透明度の設定
gl_FragColor = vec4(1.0, 0.0, 0.0, fresnel); // 赤色にフレネル効果を適用
}
スペキュラー効果
光源からの光の反射の角度に基づく鏡面反射の強さ
*用途:金属、ガラス、プラスチックなどの光沢のある素材がリアルに見えるようになる
*スペキュラー効果はライトの実装に必要
反射ベクトルと視点ベクトルのドット積でスペキュラー強度を計算
- 反射ベクトル
物体表面の法線ベクトル(normal)と、光源からその表面に向かうベクトル(lightDirection)を使って、反射ベクトル(lightReflection)を計算 - 視点ベクトル(カメラ方向)
カメラの方向から物体を見るための視点ベクトル(viewDirection) - スペキュラー強度
視点ベクトルと反射ベクトルのドット積を使って、カメラに向かって反射している光の強さを決定
視点ベクトルと反射ベクトルが一致するほど強い反射
ドット積の値が1に近いほど反射が強くなり、0に近いほど反射が弱くなる
このドット積に対してpow()を使うことで、反射の鋭さ(ハイライトの広がり具合)を調整
ライト(ディレクショナルライト・ポイントライト)の実装
ディレクショナルライトは光源からの距離を考慮せず、光の方向のみを使って光を当てる
ポイントライトはポイントライトは、光源からの距離に基づいて光の強さが減衰
varying vec3 vPosition;
varying vec3 vNormal;
// ディレクショナルライトの関数
vec3 directionalLight(vec3 lightColor, float lightIntensity, vec3 normal, vec3 lightDirection, vec3 viewDirection, float specularPower) {
// 光の方向を正規化
lightDirection = normalize(lightDirection);
// 法線ベクトルと光の方向ベクトルのドット積
// ランバートの拡散反射(Diffuse Lighting)を計算
float diffuseFactor = max(dot(normal, lightDirection), 0.0); // 法線と光の方向のドット積が負の値になる場合は0にする
// 反射ベクトルの計算 (reflect関数で光の反射方向を求める)
vec3 reflectDir = reflect(-lightDirection, normal);
// 視点ベクトルと反射ベクトルのドット積を使ってスペキュラー反射を計算
float specularFactor = max(dot(viewDirection, reflectDir), 0.0);
specularFactor = pow(specularFactor, specularPower); // スペキュラー反射の鋭さを調整
// 拡散反射とスペキュラー反射を組み合わせて最終的なライトの強度を計算
vec3 lightEffect = lightColor * lightIntensity * (diffuseFactor + specularFactor);
return lightEffect;
}
// ポイントライトの関数
vec3 pointLight(vec3 lightColor, float lightIntensity, vec3 normal, vec3 lightPosition, vec3 viewDirection, float specularPower, vec3 fragPosition, float lightDecay) {
// フラグメントの位置から光源へのベクトルを計算
vec3 lightDirection = normalize(lightPosition - fragPosition);
// 光源からフラグメントまでの距離
float lightDistance = length(lightPosition - fragPosition);
// 減衰(距離が遠いほど光が弱くなる)
float attenuation = 1.0 / (1.0 + lightDecay * lightDistance * lightDistance);
// 拡散反射(ランバートシェーディング)の強度
float diffuseFactor = max(dot(normal, lightDirection), 0.0);
// 反射ベクトルの計算
vec3 reflectDir = reflect(-lightDirection, normal);
// スペキュラー反射の強度
float specularFactor = max(dot(viewDirection, reflectDir), 0.0);
specularFactor = pow(specularFactor, specularPower);
// 拡散反射とスペキュラー反射を加算し、減衰を適用
vec3 lightEffect = lightColor * lightIntensity * attenuation * (diffuseFactor + specularFactor);
return lightEffect;
}
void main(){
// フラグメントシェーダー内でライト計算
vec3 normal = normalize(vNormal); // 法線を正規化
vec3 viewDirection = normalize(cameraPosition - vPosition); // オブジェクト位置からカメラへのベクトル
/*
アンビエントライト(環境光)の設定
物体全体に均等に光を当てる
*/
vec3 ambientLightColor = vec3(0.1, 0.1, 0.1); // 暗いグレー
float ambientIntensity = 1.0;
vec3 ambientEffect = ambientLightColor * ambientIntensity;
// ディレクショナルライトの設定
vec3 lightDir = vec3(0.0, -1.0, 0.0); // ディレクショナルライトの方向
vec3 directionalLightColor = vec3(1.0, 0.9, 0.8); // 白(太陽光)
float directionalLightIntensity = 1.0; // ディレクショナルライトの強度
float specularPower = 32.0; // スペキュラー反射の鋭さ
// ポイントライトの設定
vec3 pointLightPosition = vec3(0.0, 0.0, 5.0); // ポイントライトの位置
vec3 pointLightColor = vec3(1.0, 0.1, 0.1); //赤
float pointLightIntensity = 1.0; // ポイントライトの強度
float lightDecay = 0.1; // ポイントライトの減衰率
// ディレクショナルライトの効果
vec3 directionalLightEffect = directionalLight(directionalLightColor, directionalLightIntensity, normal, lightDir, viewDirection, specularPower);
// ポイントライトの効果
vec3 pointLightEffect = pointLight(pointLightColor, pointLightIntensity, normal, pointLightPosition, viewDirection, specularPower, vPosition, lightDecay);
// アンビエントライトとディレクショナルライトとポイントライトの効果を合算
vec3 LightEffect = ambientEffect;
LightEffect += directionalLightEffect;
LightEffect += pointLightEffect;
// 最終的な色を決定(物体の色に光の効果を乗算)
vec3 objectColor = vec3(0.5, 0.5, 1.0);
vec3 finalColor = objectColor * LightEffect;
gl_FragColor = vec4(finalColor, 1.0);
}
余談:スペキュラー反射でもフレネル効果でも、ドット積を計算するのでベクトルの向き(vPosition – cameraPosition でも cameraPosition – vPosition)はどちらでもいい
*ドット積は2つのベクトル間の角度に依存するため、ベクトルの向きが逆でも同じ角度なら結果は同じ
ハーフトーンシェーディング
- ハーフトーンシェーディングは、3Dグラフィックスやデジタルアートで、物体に陰影を与えるために、ドットのサイズや密度を変化させることで明暗を表現
レトロなコミックスタイルなどで使われることが多い - ハーフトーンシェーディングでの陰影は、一般的には光源の方向と物体の法線ベクトルとの角度をもとに決定される
varying vec3 vPosition;
varying vec3 vNormal;
uniform vec2 uResolution;
//ハーフトーンパターンを作成する関数
vec3 halftone(
vec3 color, // オブジェクトの元の色
float repetitions, // ハーフトーンのドットパターンの繰り返し回数
vec3 direction, // ライトの方向ベクトル
float low, // 照明の最小強度(スムーズに補間するための閾値)
float high, // 照明の最大強度(スムーズに補間するための閾値)
vec3 pointColor, // ハーフトーンのドットの色
vec3 normal // フラグメントの法線ベクトル(光の当たり具合に影響)
){
// 光の強度(法線と光の方向のドット積を計算)
float intensity = dot(normal, direction);
// smoothstepで光の強度を滑らかに補間
// lowからhighまでの範囲で、光の当たり具合(intensity)を滑らかにリマップ
intensity = smoothstep(low, high, intensity);
// フラグメントの画面座標(解像度に基づいてUV座標を作成)
vec2 uv = gl_FragCoord.xy / uResolution.y;
// 繰り返しパターンを作成
uv = fract(uv * repetitions) - 0.5;
// ドットパターンの中心からの距離を計算
float point = length(uv);
// step関数で点を決定。光の強度に基づいてドットのサイズを決定し、強度が大きいほどドットが大きくなる
point = 1.0 - step(0.5 * intensity, point);
// 元の色とドットの色(pointColor)を混ぜ合わせ、ドットの部分にpointColorを適用
return mix(color, pointColor, point);
}
void main(){
vec3 normal = normalize(vNormal); // 法線を正規化
vec3 viewDirection = normalize(cameraPosition - vPosition); // 視点ベクトル
//2つの異なるハーフトーンパターン(カメラの方向とライトの方法)を作成し、それを合成する例
vec3 objectColor = vec3(0.1, 0.1, 1.0);
vec3 viewColor = halftone(
objectColor, // オブジェクトの色(青色)
100.0, // ドットの繰り返し回数
viewDirection, // 視点ベクトル
-0.8, // 最小強度
1.5, // 最大強度
vec3(1.0, 0.1, 0.1), // ドットの色(赤色)
normal // フラグメントの法線
);
vec3 lightColor = halftone(
objectColor, // オブジェクトの色(青色)
100.0, // ドットの繰り返し回数
vec3(0.0, -1.0, 0.0), // ライトの方向
-0.8, // 最小強度
1.5, // 最大強度
vec3(0.1, 1.0, 0.1), // ドットの色(緑色)
normal // フラグメントの法線
);
// ハーフトーンをブレンド 例ではライト方向の影響を70%に
vec3 finalColor = mix(viewColor, lightColor, 0.7);
gl_FragColor = vec4(finalColor, 1.0);
//gl_FragColor = vec4(viewColor, 1.0);
//gl_FragColor = vec4(lightColor, 1.0);
}
THREE.Points
平面Geometry(2D)やBufferGeometryの頂点を
THREE.Points を使って頂点ごとに点を描画する
頂点ごとに点を描画
3Dジオメトリやモデルの頂点をそのまま
THREE.Pointsを使って頂点ごとに点を描画する
JSのセットアップ
import * as THREE from 'three'
import { OrbitControls } from 'three/examples/jsm/controls/OrbitControls.js'
import vertexShader from './vertex.glsl'
import fragmentShader from './fragment.glsl'
const canvas = document.querySelector('.webgl')
const scene = new THREE.Scene()
const sizes = {
width: window.innerWidth,
height: window.innerHeight,
pixelRatio: Math.min(window.devicePixelRatio, 2)
}
sizes.resolution = new THREE.Vector2(sizes.width*sizes.pixelRatio, sizes.height*sizes.pixelRatio)
const camera = new THREE.PerspectiveCamera(25, sizes.width / sizes.height, 0.1, 100)
camera.position.set(0, 0, 6)
scene.add(camera)
// Controls
const controls = new OrbitControls(camera, canvas)
controls.enableDamping = true
const renderer = new THREE.WebGLRenderer({
canvas: canvas,
antialias: true
})
renderer.setSize(sizes.width, sizes.height)
renderer.setPixelRatio(sizes.pixelRatio)
//マテリアル
const material = new THREE.ShaderMaterial({
vertexShader: vertexShader,
fragmentShader: fragmentShader,
uniforms:{
uSize: { value: 0.1 },
uResolution: { value: sizes.resolution },
},
blending: THREE.AdditiveBlending,
transparent:true,
depthWrite: false
})
//ジオメトリ
const geometry = new THREE.TorusKnotGeometry(0.6, 0.25, 128, 16)
const points = new THREE.Points(geometry, material)
scene.add(points)
function handleResize(){
sizes.width = window.innerWidth
sizes.height = window.innerHeight
sizes.pixelRatio = Math.min(window.devicePixelRatio, 2)
sizes.resolution.set(sizes.width*sizes.pixelRatio, sizes.height*sizes.pixelRatio)
camera.aspect = sizes.width / sizes.height
camera.updateProjectionMatrix()
renderer.setSize(sizes.width, sizes.height)
renderer.setPixelRatio(sizes.pixelRatio)
}
const clock = new THREE.Clock()
const tick = () =>{
controls.update()
const elapsedTime = clock.getElapsedTime()
points.rotation.x = - elapsedTime * 0.5
points.rotation.y = elapsedTime * 1
renderer.render(scene, camera)
window.requestAnimationFrame(tick)
}
handleResize()
tick()
window.addEventListener('resize', handleResize)uniform vec2 uResolution;
uniform float uSize;
void main(){
vec4 modelPosition = modelMatrix * vec4(position, 1.0);
vec4 viewPosition = viewMatrix * modelPosition;
vec4 projectedPosition = projectionMatrix * viewPosition;
gl_Position = projectedPosition;
/*
パーティクルのサイズを画面の縦方向のサイズに比例させる
*/
gl_PointSize = uSize * uResolution.y;
/*
sizeAttenuation(カメラからの距離に応じてどのように変化するかを制御))の実装
*/
gl_PointSize *= (1.0 / - viewPosition.z);
}void main(){
vec2 uv = gl_PointCoord - 0.5;
float d = length(uv);
float alpha = 0.05 / d - 0.05*2.0;
gl_FragColor = vec4(vec3(1.0), alpha);
}
「インデックス」について
インデックスはオブジェクトを構成する 三角形の頂点データを効率よく再利用するために使われます
Three.jsのジオメトリは、通常インデックスバッファを使って頂点データを再利用します
パーティクルシステムでは、三角形を描画しないものの、インデックスの仕組みによって同じ位置に複数のパーティクルが配置されることがある
*特にグリッド状の配置では、1つの頂点が複数の三角形で共有され、1つの場所に最大6つのパーティクルが配置される場合があります
const geometry = new THREE.TorusKnotGeometry(0.6, 0.25, 128, 16)
//ジオメトリでインデックスを削除
geometry.setIndex(null)
パーティクルのモーフィング(別の形状に変形)
*パーティクルの位置や属性をJavaScriptで更新する(CPUを使う)とパフォーマンスが低下するため、シェーダーを活用する
3Dジオメトリやモデルから頂点データを取得して作成したBufferGeometryの頂点を
THREE.Points を使って頂点ごとに点を描画する
TorusKnotGeometryとSphereGeometry の2つのジオメトリに対し、最大の頂点数に合わせて、少ない方の頂点をランダムに補完して作成した「adjustedPositions」を使用して BufferGeometryを作成
これを Points オブジェクトとしてシーンに追加
// TorusKnotGeometryとSphereGeometryを作成
const torusKnot = new THREE.TorusKnotGeometry(0.6, 0.25, 128, 16);
torusKnot.setIndex(null); // インデックスをnullに設定して、全ての頂点がユニークになるようにする
const sphere = new THREE.SphereGeometry(0.8, 64, 32);
sphere.setIndex(null); // 同様にインデックスをnullに設定
// geometrys配列に2つのジオメトリを格納
const geometrys = [sphere, torusKnot];
// それぞれのジオメトリのposition属性の配列を取得
const positionArrays = geometrys.map(geometry => geometry.attributes.position.array);
// 各position配列の頂点数(x, y, zの3つの成分ごとに分けて数える)を取得
const counts = positionArrays.map(positionArray => positionArray.length / 3);
// 最大の頂点数を計算
const maxCount = Math.max(...counts); // 最大のcountを取得
// adjustedPositions(ジオメトリの頂点データをmaxCountに合わせて作成)
const adjustedPositions = positionArrays.map(positionArray => {
const count = positionArray.length / 3;
if (count < maxCount) {
// 頂点数が少ない場合、ランダムな頂点を複製して頂点数を増やす
return adjustPositions(positionArray, maxCount);
}
return positionArray; // 頂点数がmaxCountに等しい場合はそのまま
});
//console.log(adjustedPositions)
// BufferGeometryを作成し、adjustedPositionsをposition属性として設定
const geometry = new THREE.BufferGeometry();
const positionAttribute = new THREE.BufferAttribute(adjustedPositions[0], 3);
geometry.setAttribute('position', positionAttribute);
// Pointsオブジェクトを作成し、シーンに追加
const points = new THREE.Points(geometry, material);
scene.add(points);
// positionArrayを受け取り、頂点数をtargetCountに増やす関数
function adjustPositions(positionArray, targetCount) {
let currentCount = positionArray.length / 3; // 現在の頂点数
let newArray = new Float32Array(targetCount * 3); // targetCountに合わせた新しい配列を作成(x, y, zの3成分)
// 既存の頂点を新しい配列にコピー
for (let i = 0; i < currentCount; i++) {
newArray[i * 3] = positionArray[i * 3]; // x
newArray[i * 3 + 1] = positionArray[i * 3 + 1]; // y
newArray[i * 3 + 2] = positionArray[i * 3 + 2]; // z
}
// 足りない部分はランダムに既存の頂点を複製して埋める
for (let i = currentCount; i < targetCount; i++) {
let randomIndex = Math.floor(Math.random() * currentCount); // ランダムに既存の頂点を選ぶ
newArray[i * 3] = positionArray[randomIndex * 3]; // x
newArray[i * 3 + 1] = positionArray[randomIndex * 3 + 1]; // y
newArray[i * 3 + 2] = positionArray[randomIndex * 3 + 2]; // z
}
return newArray; // 調整後の頂点配列を返す
}取得した adjustedPositions の2つの頂点位置(position と aPositionTarget)の間で、GSAP を使ってアニメーションを行い、シェーダーを用いて頂点の移動を実現する
import gsap from 'gsap' //GSAP追加
//省略
// シェーダーマテリアル
const material = new THREE.ShaderMaterial({
//省略
uniforms: {
//省略
uProgress: { value: 0 } // 進捗(0から1にかけてアニメーションする)
},
//省略
});
// gsap使用してuProgressの値をアニメーション
gsap.to(material.uniforms.uProgress, {
value: 1,
duration: 3,
ease: "linear",
delay:1
}
)
// 省略部分: adjustedPositionsを取得するコード
const geometry = new THREE.BufferGeometry(); // 新しいBufferGeometryを作成
const positionAttribute = new THREE.BufferAttribute(adjustedPositions[0], 3); // 元の頂点位置を格納したBufferAttribute
const targetPositionAttribute = new THREE.BufferAttribute(adjustedPositions[1], 3); // 目標となる頂点位置を格納したBufferAttribute
// ジオメトリに位置データを設定
geometry.setAttribute('position', positionAttribute); // 初期位置(position)
geometry.setAttribute('aPositionTarget', targetPositionAttribute); // 目標位置(aPositionTarget)
// Pointsオブジェクトを作成してシーンに追加
const points = new THREE.Points(geometry, material); // geometryとmaterialを持つPointsオブジェクトを作成
scene.add(points); // シーンに追加uniform vec2 uResolution; // 画面の解像度
uniform float uSize; // 各ポイントのサイズ
uniform float uProgress; // アニメーションの進捗(0から1まで)
attribute vec3 aPositionTarget; // 目標の頂点位置
void main() {
// uProgressの値に基づいて、元の頂点位置と目標頂点位置を線形補間
float progress = uProgress;
vec3 mixedPosition = mix(position, aPositionTarget, progress); // positionからaPositionTargetに向かって変化
//mixedPositionを設定
vec4 modelPosition = modelMatrix * vec4(mixedPosition, 1.0);
vec4 viewPosition = viewMatrix * modelPosition;
vec4 projectedPosition = projectionMatrix * viewPosition;
gl_Position = projectedPosition;
gl_PointSize = uSize * uResolution.y;
gl_PointSize *= (1.0 / - viewPosition.z);
}
備考
Blenderでモデル(例えばテキストなど)を作成する場合、テキストや複雑な形状では、頂点が密集している部分と直線的で少ない部分が存在します
Blenderで頂点を均等に配置するには
リメッシュモディファイアやサブディビジョンモディファイアを使って直線部分やカーブ部分にも均等に頂点が分布するように調整します

