Three.jsシェーダー・チートシート（平面ジオメトリでの実装・2D）

目次

セットアップ
パターン・図形の描画
色をつける
アニメーションのヒント
頂点シェーダー

セットアップ

THREE.PlaneGeometry（平面）を利用してスクリーンスペースに描画（カメラやモデルの位置に関係なくcanvas要素に対して直接描画）
＊特別なカメラ設定は不要、最低限のカメラを設定してシーンに追加
＊canvas要素のアスペクト比によって変形

<canvas class="webgl"></canvas>
<style>
*{
    margin: 0;
    padding: 0;
}
html,body{
    overflow: hidden;
}
.webgl{
    position: fixed;
    top: 0;
    left: 0;
    outline: none;
}
</style>

import * as THREE from 'three'
import vertexShader from './vertex.glsl'
import fragmentShader from './fragment.glsl'

const canvas = document.querySelector('.webgl')
//Sizes
const sizes = {
    width: window.innerWidth,
    height: window.innerHeight
}
const scene = new THREE.Scene()
const material = new THREE.ShaderMaterial({
    vertexShader: vertexShader,
    fragmentShader: fragmentShader,
    wireframe: true,　//試しにワイアーフレームで表示、後で削除
    uniforms:{
        uTime: { value: 0 },
        uResolution: {value: new THREE.Vector2(sizes.width, sizes.height) },
    }
})
const geometry = new THREE.PlaneGeometry(1.5,1.5) //2で全画面
const mesh = new THREE.Mesh(geometry, material)
scene.add(mesh)
const camera = new THREE.Camera();
scene.add(camera)
const renderer = new THREE.WebGLRenderer({
    canvas: canvas,
})
function handleResize(){
    sizes.width = window.innerWidth
    sizes.height = window.innerHeight
    renderer.setSize(sizes.width, sizes.height)
    renderer.setPixelRatio(Math.min(window.devicePixelRatio, 2))
    material.uniforms.uResolution.value.set(sizes.width, sizes.height);
}
const clock = new THREE.Clock()
const tick = () =>{
  const elapsedTime = clock.getElapsedTime()
  material.uniforms.uTime.value = elapsedTime
  renderer.render(scene, camera)
  window.requestAnimationFrame(tick)
}
handleResize()
tick()
window.addEventListener('resize', handleResize)

varying vec2 vUv;
void main(){
    gl_Position = vec4(position, 1.0);
    vUv = uv;
}

uniform vec2 uResolution;
uniform float uTime;
varying vec2 vUv;
void main() {
/*
vUv * 2.0 は[0,1]を[0,2]の範囲に拡張
vUv * 2.0 - 1.0 はさらに1を引くことで、座標系を [-1,1] の範囲に移動
中心が(0,0)の座標系に変換
x座標をアスペクト比でスケーリングし、y座標はそのまま
*/
  vec2 uv = (vUv * 2.0 - 1.0) * vec2(uResolution.x / uResolution.y, 1.0);

// 下記の場合はスケルールせずに、UV座標の範囲を [-0.5, 0.5] に
//vec2 uv = (vUv - 0.5) * vec2(uResolution.x / uResolution.y, 1.0);

  vec4 col = vec4(1.0,  0.0, 0.0, 1.0);// 赤色
  gl_FragColor =  col;
}

パターン・図形の描画

パターン

グリッド
fract() 関数：1.0で割った余りを返す（浮動小数点数の小数部分のみ）
＊mod() 関数：第一引数を第二引数で割った余りを返す
基準点を調整する（オフセット）
-0.5することで範囲を0から1を-0.5から0.5に

vUvの各成分に適用されたスケーリングを考慮する

vec2 uv = (vUv * 2.0 - 1.0) * vec2(uResolution.x / uResolution.y, 1.0);
vec3 col = vec3(1.0);
float s = 2.0; //UV座標をスケール（パターンがスケール倍繰り返される）
vec2 gv = fract(uv * s) - 0.5;
//vec2 gv = mod(uv*s,  1.0)- 0.5;

if(gv.x > 0.45 || gv.y > 0.45) col = vec3(0.0);
gl_FragColor =  vec4(col, 1.0);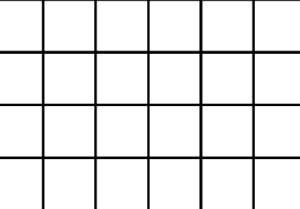

step() 関数：特定のしきい値を基に0または1の値を生成する
第一引数はしきい値、第二引数は入力値
入力値がしきい値より小さい場合は0、大きい場合は1を返す
＊1.0 - step()：しきい値よりも小さい場合は1、それ以外の場合は0

float strength = step(0.45, gv.y);
//float strength =  gv.y < 0.45 ? 0.0 : 1.0;
strength += step(0.45, gv.x);
//strength +=  gv.x < 0.45 ? 0.0 : 1.0;

gl_FragColor = vec4(vec3(strength), 1.0);

乗算は元の値をは「縮小」や「調整」する効果があり
加算は元の値を「増やす」効果がある
＊グレースケールで考えると乗算は値を黒に近づけ、加算は値を白に近づける
＊abs() 関数：絶対値を取る（引数の正負を問わず正の値を返す）

vec2 uv = (vUv * 2.0 - 1.0) * vec2(uResolution.x / uResolution.y, 1.0);
float s = 2.0;
vec2 gv = fract(uv * s) - 0.5;  //グリッド用

float strength = abs(gv.y);
strength += abs(gv.x);  //加算

gl_FragColor = vec4(vec3(strength), 1.0);

float strength = abs(gv.y);
strength *= abs(gv.x);  //乗算

max()とmin()関数は2つの数値を引数として受け取り
max()：大きい方の値を返す
min()：小さい方の値を返す

float strength  =  max(abs(gv.y),abs(gv.x));

float strength  =  min(abs(gv.y),abs(gv.x));

length() 関数：ベクトル uv の長さを計算
＊ベクトルが原点からどれだけ離れているか

vec2 uv = (vUv * 2.0 - 1.0) * vec2(uResolution.x / uResolution.y, 1.0);

float strength = length(uv);
//float strength = 1.0 - length(uv);

distance() 関数：2点間の距離を計算

float strength = distance(gv, vec2(0.0));
//float strength = length(gv);

逆距離減衰
近ければ近いほど効果が強く、遠ければ遠いほど効果が弱くする

float strength = 0.02 / length(gv);

指数関数

exp(x)関数：自然対数の底e（約 2.71828）を使用して指数計算$e^x$
自然現象や物理的な過程のモデリングに適している
exp(x) はx が増加するにつれて急速に増加する関数
exp(-x) は x が増加するにつれて急速に0に近づく関数
pow(base, x)関数：一般的な形の指数関数$base^x$

float s = 10.0;
vec2 gv = fract(uv * s) - 0.5;
//原点から距離に基づいて値が急速に増加
gv*=exp(length(uv)) ;
float strength = length(gv);

gv *= pow((length(uv)), 2.0);

floor関数 ：小数点以下で切り捨て
＊round関数は数値を四捨五入

float strength = floor(vUv.x * 10.0) / 10.0;

floor関数を使って各セルに対する整数IDを生成する
例ではuvの範囲が -1.0 から 1.0でy軸はスケーリングしていないので、id.yは-5, -4, -3, -2, -1, 0, 1, 2, 3, 4
＊黒いところはXとYがマイナス

float s = 5.0;
vec2 gv = fract(uv * s) - 0.5;
vec2 id = floor(uv * s);
vec3 col = vec3(vec2(id * 0.1), 0.0);

図形

smoothstep(A, B, x)関数（A < Bの時：0から1への滑らかな補完）
0.5 未満の場合は 0、0.7 より大きい場合は 1、その間では 0 から 1

float strength = smoothstep(0.5, 0.7, length(uv));

備考：ある範囲の数値を滑らかに 0 から1へとリマップしたい場合などに利用

//value を -1.0から1.0 の範囲で滑らかに 0から1 にリマップ
float value = smoothstep(-1.0, 1.0, value);

smoothstep関数の引数の順序を逆転（A > Bの時：1から0への滑らかな補完）
0.7 未満の場合は 1、0.5 より大きい場合は 0、その間では 1 から 0 へと滑らかに変化

float strength = smoothstep(0.7, 0.5, length(uv));
//float strength = 1.0 - smoothstep(0.5, 0.7, length(uv));と同じ

スケーリング
uv.y*2.0でy座標を広げる（座標系の中心からの距離増加）
d*2.0でズームアウト効果

float d = length(vec2(uv.x, uv.y*2.0));
float strength = smoothstep(0.5, 0.49, d*2.0);

uv.xを累乗する

float d = length(vec2(uv.x, uv.y - uv.x * uv.x)); 
float strength = smoothstep(0.7, 0.5, d);

備考：desmos（式を打ち込むとグラフを表示してくれる）

lengthの応用
length(uv)は、length(uv-vec2(0.0, 0.0))と同じ
＊ベクトルが原点からどれだけ離れているか

//uv.yの値を -0.3と0.3の範囲
float d = length(uv-vec2(0.0, clamp(uv.y,-0.3, 0.3)));
//float d = distance(uv, vec2(0.0, clamp(uv.y,-0.3, 0.3)));
//rでサイズを調整
float r = 0.1;
float strength = smoothstep(0.1, 0.0, d-r);

「xの絶対値」を利用する：中心に近いほどある種の変化や効果を適用できる
＊xが中心に近い場合xの絶対値が小さくなる
V字型に変形する例
y座標からx座標の絶対値を使用して引いて減少（上方向への移動）させる
y座標の変化はxが中心に近いほど少なく、中心から遠いほど大きくなる

float d = length(vec2(uv.x, uv.y - abs(uv.x)));
float strength = smoothstep(0.7, 0.5, d);

絶対値を利用して処理をまとめたり、左右対称にしたり

//原点から半径0.3の円の内外での距離の差を取りその絶対値を計算
float strength = smoothstep(0.05, 0.01, abs(length(uv) - 0.3));

float strength = smoothstep(0.05, 0.0, abs(abs(uv.x)-0.5));

float strength = smoothstep(0.05, 0.0, abs(abs(uv.x)-smoothstep(0.0, 1.0, uv.y )));

四角形を描画するRect関数を作成

//bottomLeft と topRight は矩形の左下と右上を指定するベクトル
float Rect(vec2 uv, vec2 bottomLeft, vec2 topRight, float blur) {
    blur = max(blur, 0.0);
    float leftEdge = smoothstep(bottomLeft.x - blur, bottomLeft.x + blur, uv.x);
    float rightEdge = smoothstep(topRight.x + blur, topRight.x - blur, uv.x);
    float bottomEdge = smoothstep(bottomLeft.y - blur, bottomLeft.y + blur, uv.y);
    float topEdge = smoothstep(topRight.y + blur, topRight.y - blur, uv.y);
    return min(leftEdge, rightEdge) * min(bottomEdge, topEdge);
}

//使用例
float x = uv.x;
float y = uv.y;
float strength =  Rect(vec2(x,y), vec2(-0.3, -0.3), vec2(0.3, 0.3), 0.01);
gl_FragColor =  vec4(vec3(strength), 1.0);

x += y;

y -=(x - 0.5)*(x + 0.5);


float strength =  Rect(vec2(x,y), vec2(-0.3+ y, -0.3 ), vec2(0.3 - y, 0.3),0.01);

六角形を作成する関数

float HexDist(vec2 p) {
	p = abs(p);  
    float c = dot(p, normalize(vec2(1,1.73)));
    c = max(c, p.x);   
    return c;
}

//使用例
float d = HexDist(uv);
float strength = smoothstep(0.5, 0.49 , d);
gl_FragColor = vec4(vec3(strength), 1.0);

六角形のグリッドを作成する関数

// 戻り値: xは角度、yは距離(極座標)、id.xとid.yはグリッド内のセルの位置
vec4 HexCoords(vec2 uv) {
	vec2 r = vec2(1, 1.73);
    vec2 h = r*.5;
    vec2 a = mod(uv, r)-h;
    vec2 b = mod(uv-h, r)-h;
    vec2 gv = dot(a, a) < dot(b,b) ? a : b;
    float x = atan(gv.x, gv.y);
    x = (x+3.14)/6.28;
    float y = HexDist(gv);
    vec2 id = uv-gv;
    return vec4(x, y, id.x,id.y);
}

//使用例
float s = 2.0;
vec4 gv = HexCoords(uv*s);
float strength = smoothstep(.01, .03, gv.y);
gl_FragColor = vec4(vec3(strength), 1.0);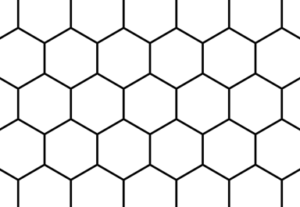

星形を作成する関数

float Star(vec2 uv, float size) {
    uv.x = abs(uv.x);
    float a = 6.2832/5.0;
    float d1 = dot(uv, vec2(sin(a), cos(a)));
    a = 3.0*6.2832/5.0;
    float d2 = dot(uv, vec2(sin(a), cos(a)));
    a = 2.0*6.2832/5.0;
    float d4 = dot(uv, vec2(sin(a), cos(a)));
    float d = min(max(d1, d2), max(uv.y, d4));
    float w = min(fwidth(d), 0.05);
    return smoothstep(w, -w, d-size);
}

//使用例
 float strength = Star(uv, 0.08);

その他

uv座標を矩形の左下隅を原点とする座標系に変換する便利関数「In」作成
矩形内の座標に描画する

vec2 In(vec2 uv, vec4 rect) {
    //矩形の幅と高さを計算し、0での除算を防ぐために非常に小さい値でクランプ
    vec2 size = max(rect.zw - rect.xy, vec2(0.0001));
    // UV座標を矩形の左下角からの相対座標に変換し、矩形のサイズで正規化
    return (uv - rect.xy) / size;
}

//使用例 矩形の左下xy、右上xx
 vec2 uv1 =  In(uv, vec4(-0.5, -0.5, -0.1, -0.1));
 vec2 uv2 =  In(uv, vec4(0.1, 0.1, 0.5, 0.5 ));
//矩形内で中心を原点に
 float d1 = length(uv1-vec2(0.5));
 float d2 = length(uv2-vec2(0.5));

 float strength =  smoothstep(0.5, 0.4, d1);
 strength+=  smoothstep(0.5, 0.4, d2);

atan(y, x) 関数：点 (x, y)から原点までの角度（ラジアン）を計算し -π(-3.14…) から π (3.14…)の範囲で返す
-πからπ を 0から1の範囲にしたい場合は正規化する
sin() 関数の出力範囲は -1から1、繰り返しを多くするために波の周波数を上げる

float angle = atan(uv.y, uv.x);
//float strength = (angle + 3.14) / (2.0 * 3.14);  //正規化

float strength = sin(angle * 10.0);

極座標系：直交座標 (x, y) とは異なり、ある点Pは (r, θ)で表す

半径 (r): 原点（基準点）から点までの距離
角度 (θ): 原点から点への線が、x軸の正方向と成す角度

直交座標で作成したパターンを極座標系にする

vec2 uv = (vUv * 2.0 - 1.0) * vec2(uResolution.x / uResolution.y, 1.0);
//極座標系にする
uv = vec2(atan(uv.y, uv.x), length(uv));
//正規化する場合
//uv.x = (uv.x + 3.14) / 6.28;
float s = 3.0;
vec2 gv = fract(uv * s) - 0.5;
float strength  =  max(abs(gv.y),abs(gv.x));
gl_FragColor = vec4(vec3(strength), 1.0);

色をつける

gl_FragColor =  vec4(vUv, 1.0, 1.0);

mix() 関数：二つの値またはベクトルを指定された割合で補間（線形補間）
＊戻り値は 0 から1の範囲に限定されないので、必要に応じて0.0から1.0の範囲にクランプする

float strength = floor(vUv.x * 30.0) / 30.0;
vec3 color1 = vec3(0.0, 0.0, 1.0);  //青
vec3 color2 = vec3(1.0, 0.0, 0.0);  //赤
vec3 mixedColor = mix(color1, color2, strength);
gl_FragColor =  vec4(mixedColor, 1.0);

備考：mix関数を使ってある範囲の値を別の範囲にリマップする例と注意点
＊originalValueが 0未満や1を超える値である場合、mix 関数は動作するが結果としてx yの範囲を超えた値が生成される

float originalValue = 0.5; // 元の範囲は0から1
float remappedValue = mix(10.0, 20.0, originalValue); //remappedValueは15になる

色のパレット関数を使う

グラデーションを変更する場合の参考サイト

vec3 palette(float t) {
    vec3 a = vec3(0.5, 0.5, 0.5);
    vec3 b = vec3(0.5, 0.5, 0.5);
    vec3 c = vec3(1.0, 1.0, 1.0);
    vec3 d = vec3(0.000, 0.333, 0.667);
    return a + b * cos(6.28318 * (c * t + d));
}

float strength = floor(vUv.x * 36.0) / 36.0;
vec3 col = palette(strength);
gl_FragColor =  vec4(col,1.0);

マスクする　（乗算）
白い部分（値が1）：通常、白い部分は完全に「下にある層が表示」される
黒い部分（値が0）：黒い部分は「下にある層が隠される」

float d = length(vec2(uv.x, uv.y));
float mask = smoothstep(0.7, 0.8, d);
vec3 col = vec3(1.0, 0.0, 0.0); //赤
col = col * mask;

gl_FragColor =  vec4(col, 1.0);

加算
白い部分（値が1）は下にある層が隠されて、黒い部分（値が0）は下にある層が表示される

col = col + mask;

透過度を使う
＊dが0.7 未満のところでalphaが1になるのでこの領域は不透明な赤色で表示

float d = length(vec2(uv.x, uv.y));
float alpha = smoothstep(0.8, 0.7, d); //逆補完
vec3 col = vec3(1.0, 0.0, 0.0); //赤

gl_FragColor =  vec4(col, alpha);

mix(x, y, a)関数で指定したアルファ値に基づいて第一引数と第二引数の色を混ぜ合わせる
aは0から1の間の値で、a = 0 のとき x を、a = 1 のとき y を返す

vec4 Circle(vec2 uv){
     vec4 col = vec4(1.0, 1.0, 0.0, 1.0);
     float d  =  length(uv);
     col.a = smoothstep(0.5, 0.49, d);
     // 目の位置を計算
     d = length(vec2((uv.x-0.15)*1.5, uv.y-0.2));
     float eye = smoothstep(0.12,0.11, d);
     // 頬の位置を計算
     d = length(uv-vec2(0.3, 0.0));
     float cheek = smoothstep(.25,.01, d)*0.4;
     //目と頬の色を合成
     col.rgb = mix(col.rgb, vec3(0.0, 0.1, 0.1), eye);
     col.rgb = mix(col.rgb, vec3(1.0, 0.1, 0.1), cheek);
    return col;
}
vec4 Mouth(vec2 uv){
    uv -= 0.5;
	vec4 col = vec4(1.0, 0.2, 0.2, 1.0);
    uv.y -= uv.x * uv.x *2.5;
    float d = length(uv);
    col.a = smoothstep(0.5, 0.48, d);
    return col;
}
vec2 In(vec2 uv, vec4 rect) {
    vec2 size = max(rect.zw - rect.xy, vec2(0.0001));
    return (uv - rect.xy) / size;
}

void main() {
  vec2 uv = (vUv * 2.0 - 1.0) * vec2(uResolution.x / uResolution.y, 1.0);
  // 背景色を設定（灰色）
  vec4 col = vec4(0.7, 0.7, 0.7, 1.0);
  // 顔の描画 abs(uv.x)を使用して目と頬を左右対称に描画
  vec4 face = Circle(vec2(abs(uv.x), uv.y));
  //口の描画  In関数を使って矩形内の座標に描画
  vec4 mouth =  Mouth(In(uv, vec4(-0.3, -0.4, 0.3, -0.1)));
  // 顔と口と背景色を合成
  col = mix(col, face, face.a);
  col = mix(col, mouth, mouth.a);
  gl_FragColor = col;
}

ガンマ補正を行う
＊ガンマ補正の一般的なガンマ値は 2.2
元々ガンマ補正がかかっていない線形空間の色を、ガンマ補正されたディスプレイに適した色に変換する場合、色の値に 1/2.2 で0.4545 を乗じる

col = pow(col, vec4(.4545));

アニメーションのヒント

sinとcos：-1から1までの値を返す
sinは角度が0のとき0
cosは角度が0のとき1
＊0から1にしたいとき：sin() * 0.5 + 0.5
fract(uTime)：0から1未満の値を返す（uTime が 1.0 になると次は0）

リマップの式
値 x を範囲 [a, b] から新しい範囲 [c, d] に変換する場合
y = (x – a) * (d – c) / (b – a) + c

//値 x を範囲 [a, b] から新しい範囲 [c, d] に変換する関数
float remap(float x, float a, float b, float c, float d){
  return c + (x - a) * (d - c) / (b - a);
}

背景

UV座標を利用する

vec2 uv = (vUv * 2.0 - 1.0) * vec2(uResolution.x / uResolution.y, 1.0);
//結果が[0, 1]の範囲に  UV座標のスケールを調整してRGB値を計算
vec3 col = 0.5 + 0.5* sin(uTime - uv.xyx * vec3(10.0, 10.0, 20.0));
gl_FragColor = vec4(col, 1.0);

//グリット用にコピーしておく
vec2 uv0 = uv;
//極座標
uv = vec2(atan(uv.y, uv.x), length(uv));
vec3 col = 0.5 + 0.5* sin(uTime - uv.xyx * vec3(3.0, 3.0, 6.0));

float s = 5.0;
vec2 gv = fract(uv0 * s) - 0.5;
float m = abs(gv.y);
m *= abs(gv.x);

col += m;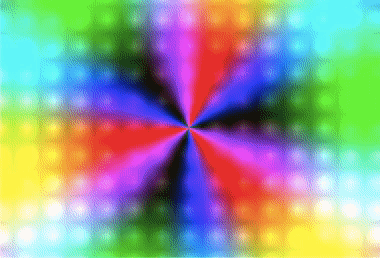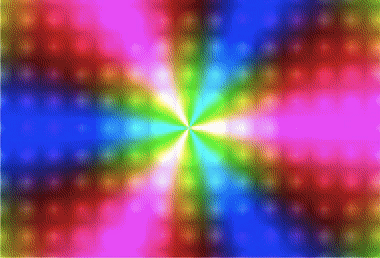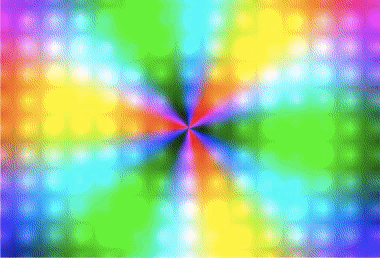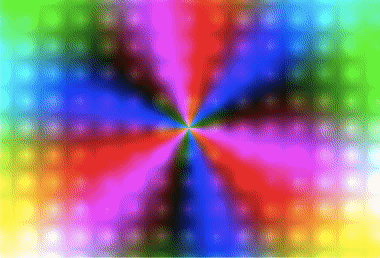

パレット関数を利用する
＊六角形関数を使ってみる

vec2 uv = (vUv - 0.5) * vec2(uResolution.x / uResolution.y, 1.0);
vec2 uv0 = uv;
vec3 col = palette(HexDist(uv0) - uTime);

//極座標　
uv = vec2(atan(uv.y, uv.x), length(uv));
uv.x = ((uv.x + 3.14) / 6.28) * 3.0;
float s = 3.0;
vec4 gv = HexCoords(uv*s);
//gv.y
float m = smoothstep(0.01, 0.9, gv.x);
m = sin(m * 10.0+ uTime) / 10.0;
m = abs(m);
m = 0.02 / m;
col *= m;

//極座標を解除して、gv.yにする
float d = smoothstep(.01, .9, gv.y);

回転と移動

2D空間での回転

/*
2D平面上の点を特定の角度で回転させるためための、2Dの回転行列を生成する関数
*/
mat2 Rot(float a) {
	float s=sin(a), c=cos(a);
    return mat2(c,-s,s,c);
}

//使用例

// 回転の中心 (cx, cy) を設定
vec2 center = vec2(0.0, -0.3);
// 回転の中心へ移動
uv -= center;
// 回転
uv *= Rot(sin(uTime));
// 元の位置へ戻す
uv += center;

float d = length(uv-vec2(0.0, clamp(uv.y,-0.3, 0.3)));
float r = 0.1;
float strength = smoothstep(0.1, 0.0, d-r);

gl_FragColor = vec4(vec3(strength), 1.0);

//絶対値を使って中心から放射状に
uv = abs(uv);
uv=(uv.x < uv.y)? uv.xy : uv.yx;
uv*=Rot(uTime* 0.3);
vec2 gv = fract(uv * 2.0) - 0.5;
float strength  =  min(abs(gv.y),abs(gv.x));

2D空間での移動

vec2 movePoint(vec2 p, vec2 dir, float t) {
    vec2 normalizedDir = normalize(dir);
    vec2 newPosition = p + t * normalizedDir;
    return newPosition;
}

//使用例
vec2 pos = movePoint(uv, vec2(0.5, 0.5), sin(uTime));
float d = length(pos);
float strength =  smoothstep(0.07, 0.05, d);

ループ

float stp = 1.0 / 5.0;
float m = 0.0;
for(float i=0.0; i<1.0; i+=stp) {
    vec2 pos = movePoint(uv, vec2(1.0, 0.0), clamp(sin(uTime + i), -0.9, 0.9));
    float d = length(vec2(pos.x , pos.y + clamp(cos(uTime + i),  -0.9, 0.9)));
    m += smoothstep(0.08, 0.07, d);
  //  m = clamp(m, 0.0, 1.0);
}
vec3 col = vec3(0.1, 1.0, 0.1) * m;
gl_FragColor = vec4(col, 1.0);

vec2 uv0 = uv;
uv = vec2(atan(uv.y, uv.x), length(uv));
uv.x = ((uv.x+3.14)/6.28) * 5.0;
vec3 col = vec3(0.1, 0.2, 0.8);
for (float i = 0.0; i < 5.0; i++) {
    uv = fract(uv * 2.0) - 0.5;
    float d = length(uv);
    vec3 c = palette(length(uv0*i) - uTime * 0.7 );
    d = 0.02 / d;
    col +=  d * c;
}
gl_FragColor = vec4(col, 1.0);

中心のセルと隣接する上下左右、対角線上のセルを含めた計9つのセルをカバーするループを使ってボロノイパターンを作成する
gv：セルの中心からの相対的な位置
id ：セルの一意の識別子
offset：周囲のセルにアクセスするための相対位置（現在のセルから見た隣接セルへのベクトル）
cid ：隣接する各セルのID
＊ボロノイパターンは、平面を点に最も近い領域に分割する方法で、各点の周りに形成される領域をボロノイセルと呼び、隣接するセルは等距離の境界で分けられる

//ランダムなvec2（0以上1未満）を返す
vec2 N22(vec2 p){
    vec3 a = fract(p.xyx*vec3(123.34,234.34, 345.65));
    a += dot(a, a+34.45);
    return fract(vec2(a.x*a.y, a.y* a.z));
}

float s = 2.0;
vec2 gv = fract(uv * s) - 0.5;
vec2 id = floor(uv * s);
//大きな距離で初期化
float minDist = 100.0;
vec2 cellIndex = vec2(0.0);
for(float y = -1.0; y<= 1.0;  y++){
    for(float x = -1.0; x <= 1.0;  x++){
        vec2 offset = vec2(x, y);

        vec2 n = N22(vec2( id + offset));
        vec2 p = offset + n;
      //  vec2 p = offset + sin(n+ uTime*0.5)*0.5;
        float d = length(gv - p);
        if(d < minDist){
            minDist = d;
            cellIndex = id + offset;
        }
    }
}
cellIndex = N22(cellIndex);
vec3 col = vec3(cellIndex, 1.0);
//vec3 = vec3(minDist, 1.0);
gl_FragColor = vec4(col, 1.0);

頂点シェーダー

カメラやモデルの位置を考慮する

//const camera = new THREE.Camera();
//scene.add(camera)

const camera = new THREE.PerspectiveCamera(75, sizes.width / sizes.height, 0.1, 100)
camera.position.set(0, 0, 1);
scene.add(camera)

function handleResize(){
　　//追加
    camera.aspect = sizes.width / sizes.height;
    camera.updateProjectionMatrix();
   //省略 
}

varying vec2 vUv;

void main(){
/*
gl_Position が変換行列を使用して設定される場合
projectionMatrix はアスペクト比を考慮しているのでuResolutionはここでは不要
フラグメントシェーダーではvUv-1.0から1.0の範囲にマッピングするだけ
vec2 uv = vUv * 2.0 - 1.0;
*/
    gl_Position = projectionMatrix * modelViewMatrix * vec4(position, 1.0);
　　// gl_Position = vec4(position, 1.0);
    vUv = uv;
}

備考：このページのスマートフォンのエフェクトはモデルの画面に平面（2：3）を組み込んで、その部分のマテリアルをシェーダーで実装

 vec2 uv = (vUv * 2.0 - 1.0);
 vec2 aspect = vec2(1.0, 1.5);
 uv *= aspect;

投影行列 (projectionMatrix)
3D空間を2Dスクリーン空間に変換します
3Dシーンが平面のディスプレイ上でどのように見えるか（遠近感や視野角など）が決まる
モデル行列 (modelMatrix)
オブジェクトの位置、回転、スケールを調整し、ワールド座標系でのその配置を決定する
ビュー行列 (viewMatrix)
カメラの視点を定義し、シーンをカメラの視点からどのように見るかを決めます
これはワールド座標系からカメラ固有の座標系への変換
モデルビュー行列 (modelViewMatrix)
modelMatrix*viewMatrix
オブジェクトがカメラに対してどの位置にあるか

//複数の頂点を使う場合はセグメント数(分割数)を増やす
onst geometry = new THREE.PlaneGeometry(1,1, 32, 32)

uniform float uTime;
varying vec2 vUv;
varying float vElevation;
void main(){
    /* 
      頂点をアニメーションする場合は分解すると分かりやすい
      gl_Position = projectionMatrix * viewMatrix  * modelMatrix * vec4(position, 1.0);
    */
    vec4 modelPosition = modelMatrix * vec4(position, 1.0); // モデル座標系へ
    
    //濃淡をつけるための変数としてフラグメントシェーダーに送る
    float elevation = sin(modelPosition.x * 5.0 + uTime ) * 0.1;
    modelPosition.y += elevation;

    vec4 viewPosition = viewMatrix * modelPosition;// ビュー座標系へ
    vec4 projectedPosition = projectionMatrix * viewPosition;// 投影座標系へ

    vUv = uv;
    vElevation = elevation;

    gl_Position = projectedPosition;
}

varying vec2 vUv;
varying float vElevation;
void main() {
    vec2 uv = (vUv * 2.0 - 1.0);
    gl_FragColor = vec4(vec3(1.0, 0.1, 0.1) * 1.0- vElevation*3.0, 1.0);
}